Illustration
Data
The subset of the data from Integrated Public Use Microdata Series (IPUMS) is used to illustrate the functionality of the package. The data are available in the package and can be loaded by
library(didnp)
library(tidyverse)
#R> ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
#R> ✔ dplyr 1.1.4 ✔ readr 2.1.5
#R> ✔ forcats 1.0.0 ✔ stringr 1.5.1
#R> ✔ ggplot2 3.5.1 ✔ tibble 3.2.1
#R> ✔ lubridate 1.9.4 ✔ tidyr 1.3.1
#R> ✔ purrr 1.0.2
#R> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#R> ✖ dplyr::filter() masks stats::filter()
#R> ✖ dplyr::lag() masks stats::lag()
#R> ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
data(Unempl, package = "didnp")
head(Unempl)
#R> FT YEAR UNEMP SEX STATEFIP SCHOOL AGE YRIMMIG EDUC AFTER ELIGIBLE
#R> 1 1 2008 5.883333 2 1 1 23 2000 6 0 1
#R> 2 1 2008 5.883333 1 1 1 27 1993 6 0 0
#R> 3 1 2008 5.883333 2 1 1 30 1980 6 0 0
#R> 4 1 2008 5.883333 1 1 1 27 1994 6 0 0
#R> 5 1 2008 5.883333 2 1 1 25 1991 6 0 1
#R> 6 1 2008 6.475000 2 2 1 24 1987 7 0 1The description of the dataset can be found by typing
?Unempl
table(Unempl$age)The variable ELIGIBLE is equal to 1 if the observation is in the treated group and 0 if in the control group.
table(Unempl$YEAR, Unempl$ELIGIBLE)
#R>
#R> 0 1
#R> 2008 848 1506
#R> 2009 816 1563
#R> 2010 851 1593
#R> 2011 779 1571
#R> 2013 747 1377
#R> 2014 707 1349
#R> 2015 623 1227
#R> 2016 629 1196Consider the treated by age
table(Unempl$ELIGIBLE, Unempl$AGE)
#R>
#R> 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
#R> 0 0 0 0 0 0 106 308 489 765 670 609 578 536 599 617
#R> 1 180 574 968 1198 1180 1123 1167 1150 1189 996 746 513 309 89 0
#R>
#R> 37 38 39
#R> 0 386 251 86
#R> 1 0 0 0Both treated and control groups must have comparable individuals. So we need to restrict the sample where age of individuals is between 27 and 35.
For convenience, a dataset with a smaller number of variables is created
d2 <- data.frame(
y = as.numeric(Unempl$FT),
year = Unempl$YEAR,
unemp = Unempl$UNEMP,
sex = factor(Unempl$SEX),
age = ordered(Unempl$AGE),
yrimmig = ordered(Unempl$YRIMMIG),
educ = ordered(Unempl$EDUC),
treatment_period = as.numeric(Unempl$AFTER),
treated = as.numeric(Unempl$ELIGIBLE)
)There is a gap in the year
table(d2$year)
#R>
#R> 2008 2009 2010 2011 2013 2014 2015 2016
#R> 2354 2379 2444 2350 2124 2056 1850 1825Year 2012 is missing from this dataset because while the treatment occurred in 2012 IPUMS does not record when the survey was filled out and we therefore do not know whether observations from 2012 are in the pre- or post-treatment time period. A variable t is generated, where
| Year | t |
|---|---|
| 2008 | -3 |
| 2009 | -2 |
| 2010 | -1 |
| 2011 | 0 |
| 2013 | 1 |
| 2014 | 2 |
| 2015 | 3 |
| 2016 | 4 |
An artificial variable period that does not have a gap is generated, where
| Year | period |
|---|---|
| 2008 | 1 |
| 2009 | 2 |
| 2010 | 3 |
| 2011 | 4 |
| 2013 | 5 |
| 2014 | 6 |
| 2015 | 7 |
| 2016 | 8 |
To make the sample more homogeneous and smaller for illustrative purposes, the subsample of the data with the following conditions is created:
age >= 27 & age <= 35yrimmig >= 1982 & yrimmig <= 1994educ >= 6 & educ <= 11
year_min <- min(Unempl$YEAR)
d0 <- d2 %>%
filter(age >= 27 & age <= 35) |>
filter(yrimmig >= 1982 & yrimmig <= 1994) |>
filter(educ >= 6 & educ <= 11) |>
mutate(
yrimmig = droplevels(yrimmig),
educ = droplevels(educ),
age = droplevels(age)
) |>
mutate(period = dplyr::if_else(year < 2012,
year - year_min + 1,
year - year_min),
t = period - min(period[treatment_period == 1]-1))
table(d0$period)
#R>
#R> 1 2 3 4 5 6 7 8
#R> 739 867 1131 1310 1356 1151 895 779Here is a basic description of the data
Treated over time
table(d0$year, d0$treated)
#R>
#R> 0 1
#R> 2008 655 84
#R> 2009 620 247
#R> 2010 641 490
#R> 2011 612 698
#R> 2013 490 866
#R> 2014 327 824
#R> 2015 175 720
#R> 2016 51 728
table(d0$t, d0$treated)
#R>
#R> 0 1
#R> -3 655 84
#R> -2 620 247
#R> -1 641 490
#R> 0 612 698
#R> 1 490 866
#R> 2 327 824
#R> 3 175 720
#R> 4 51 728Recoded variable t
table(d0$t, d0$year)
#R>
#R> 2008 2009 2010 2011 2013 2014 2015 2016
#R> -3 739 0 0 0 0 0 0 0
#R> -2 0 867 0 0 0 0 0 0
#R> -1 0 0 1131 0 0 0 0 0
#R> 0 0 0 0 1310 0 0 0 0
#R> 1 0 0 0 0 1356 0 0 0
#R> 2 0 0 0 0 0 1151 0 0
#R> 3 0 0 0 0 0 0 895 0
#R> 4 0 0 0 0 0 0 0 779Treated by the year of immigration
table(d0$yrimmig, d0$treated)
#R>
#R> 0 1
#R> 1982 129 107
#R> 1983 122 147
#R> 1984 139 214
#R> 1985 228 297
#R> 1986 183 312
#R> 1987 158 265
#R> 1988 240 371
#R> 1989 387 563
#R> 1990 579 691
#R> 1991 332 432
#R> 1992 415 415
#R> 1993 336 404
#R> 1994 323 439Treated by education
table(d0$educ, d0$treated)
#R>
#R> 0 1
#R> 6 2647 3128
#R> 7 559 845
#R> 8 178 334
#R> 10 151 301
#R> 11 36 49Treated by age
table(d0$treated, d0$age)
#R>
#R> 27 28 29 30 31 32 33 34 35
#R> 0 72 233 365 609 502 474 457 408 451
#R> 1 737 761 681 733 615 506 350 214 60Although this can be done on the fly, the subsample can be prepared beforehand:
# get the subsample
d0 <- d0 %>%
mutate(smpl = year >= 2010 & year <= 2014)
table(d0$smpl)
#R>
#R> FALSE TRUE
#R> 3280 4948Define the formula that we will use:
form1 <- y ~ age + educ + sex + unemp | period | treated | treatment_periodTo obtain standard errors and perform testing in this illustration,
we will use a few number of bootstrap replicaitons here, but we advise to set
boot.num = 399or larger in an application.
B <- 99Testing
To test if there is a violation of the bias stability condition use command didnptest
tym1test <- didnpbsctest(
form1,
data = d0,
subset = smpl,
boot.num = B,
print.level = 2,
cores = 10)
#R> Warning in didnpbsctest.default(outcome = Y, regressors = X, time = time, :
#R> Data starts in 3, while the treatment is in 4
#R> Number of Observations is 4948
#R>
#R> Number of observations in treated group right after the treatment (N_ 1, 1) = 866
#R> Number of observations in treated group just before the treatment (N_ 1, 0) = 698
#R> Number of observations in treated group one period before the treatment (N_ 1,-1) = 490
#R> Number of observations in control group right after the treatment (N_ 0, 1) = 490
#R> Number of observations in control group just before the treatment (N_ 0, 0) = 612
#R> Number of observations in control group one period before the treatment (N_ 0,-1) = 641
#R>
#R> Number of Continuous Regressors = 1
#R> Number of Unordered Categorical Regressors = 1
#R> Number of Ordered Categorical Regressors = 2
#R>
#R> Bandwidths are chosen via the plug-in method
#R>
#R> Calculating BSC
#R> BSC = 0.193390839
#R> Calculating BSC completed in 0 seconds
#R>
#R> Bootstrapping the statistic (99 replications)
#R> Calculating residuals for the alternative model
#R> Calculating residuals for the alternative model completed in 0 seconds
#R> Calculating fitted values under the null hypothesis
#R> Calculating fitted values under the null hypothesis completed in 0 seconds
#R>
#R> The main loop of the bootstrapping started
#R>
#R> Bootstrapping will take approximately: 2 seconds
#R>
#R> | |= | 1% | |= | 2% | |== | 3% | |=== | 4% | |==== | 5% | |==== | 6% | |===== | 7% | |====== | 8% | |====== | 9% | |======= | 10% | |======== | 11% | |========= | 12% | |========= | 13% | |========== | 14% | |=========== | 15% | |=========== | 16% | |============ | 17% | |============= | 18% | |============== | 19% | |============== | 20% | |=============== | 21% | |================ | 22% | |================ | 23% | |================= | 24% | |================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 29% | |===================== | 30% | |===================== | 31% | |====================== | 32% | |======================= | 33% | |======================== | 34% | |======================== | 35% | |========================= | 36% | |========================== | 37% | |========================== | 38% | |=========================== | 39% | |============================ | 40% | |============================= | 41% | |============================= | 42% | |============================== | 43% | |=============================== | 44% | |=============================== | 45% | |================================ | 46% | |================================= | 47% | |================================== | 48% | |================================== | 49% | |=================================== | 50% | |==================================== | 51% | |==================================== | 52% | |===================================== | 53% | |====================================== | 54% | |======================================= | 55% | |======================================= | 56% | |======================================== | 57% | |========================================= | 58% | |========================================= | 59% | |========================================== | 60% | |=========================================== | 61% | |============================================ | 62% | |============================================ | 63% | |============================================= | 64% | |============================================== | 65% | |============================================== | 66% | |=============================================== | 67% | |================================================ | 68% | |================================================= | 69% | |================================================= | 70% | |================================================== | 71% | |=================================================== | 72% | |=================================================== | 73% | |==================================================== | 74% | |===================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 79% | |======================================================== | 80% | |======================================================== | 81% | |========================================================= | 82% | |========================================================== | 83% | |=========================================================== | 84% | |=========================================================== | 85% | |============================================================ | 86% | |============================================================= | 87% | |============================================================= | 88% | |============================================================== | 89% | |=============================================================== | 90% | |================================================================ | 91% | |================================================================ | 92% | |================================================================= | 93% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 97% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 100%
#R> Bootstrapping the statistic completed in 2 seconds
#R> p.value:
#R> [1] 0.37
#R>
#R> BSC statistic = 0.1934
#R> BSC bootstrapped standard error = 0.04252
#R> Bootstrapped p-value = 0.37Interpretation: We do not find evidence against the null hypothesis that the bias stability condition holds. The desired p-value should be much larger than the 0.1 level.
Estimation
To estimate the average treatment effects, we use the didnpreg function. The didnpreg function allows using matrices. The manual explains how to use matrix syntax (type ?didnpreg).
Just a remainder that TTa calculates the ATET in the post-treatment period, while TTb calculated the ATET in both prior and post-treatment periods.
To speed up the estimation
on computers with multiple cores, use multiplrocessing by setting option
cores.
Suppress output by setting print.level = 0. The default value is 1.
# suppress output
tym1a <- didnpreg(
form1,
data = d0,
subset = smpl,
bwmethod = "opt",
boot.num = B,
TTx = "TTa",
print.level = 2,
digits = 8,
cores = 10)
#R> Warning in didnpreg.default(outcome = Y, regressors = X, time = time, treated =
#R> treated, : Data starts in 3, while the treatment is in 4
#R> Number of observations = 4948
#R> Number of observations in the year of the treatment and one year after the treatment = 2666
#R>
#R> Number of observations in treated group after the treatment (N_ 1, 1) = 1690
#R> Number of observations in treated group before the treatment (N_ 1, 0) = 1188
#R> Number of observations in control group after the treatment (N_ 0, 1) = 817
#R> Number of observations in control group before the treatment (N_ 0, 0) = 1253
#R>
#R> Number of Continuous Regressors = 1
#R> Number of Unordered Categorical Regressors = 1
#R> Number of Ordered Categorical Regressors = 2
#R>
#R> Bandwidths are chosen via the plug-in method
#R>
#R> Regressor Type Bandwidth
#R> 1 age ordered 9.356700e-05
#R> 2 educ ordered 9.049838e-05
#R> 3 sex factor 5.909937e-04
#R> 4 unemp continuous 2.397334e-01
#R>
#R> Calculating ATET: TTa
#R> TTa = 0.074190278, N (TTa; treated in the first period or N_ 1, 1) = 1690
#R> Calculating ATET completed in 0 seconds
#R>
#R> Bootstrapping standard errors (99 replications)
#R> Calculating residuals completed
#R>
#R> Bootstrapping will take approximately: 3 seconds
#R>
#R> | |= | 1% | |= | 2% | |== | 3% | |=== | 4% | |==== | 5% | |==== | 6% | |===== | 7% | |====== | 8% | |====== | 9% | |======= | 10% | |======== | 11% | |========= | 12% | |========= | 13% | |========== | 14% | |=========== | 15% | |=========== | 16% | |============ | 17% | |============= | 18% | |============== | 19% | |============== | 20% | |=============== | 21% | |================ | 22% | |================ | 23% | |================= | 24% | |================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 29% | |===================== | 30% | |===================== | 31% | |====================== | 32% | |======================= | 33% | |======================== | 34% | |======================== | 35% | |========================= | 36% | |========================== | 37% | |========================== | 38% | |=========================== | 39% | |============================ | 40% | |============================= | 41% | |============================= | 42% | |============================== | 43% | |=============================== | 44% | |=============================== | 45% | |================================ | 46% | |================================= | 47% | |================================== | 48% | |================================== | 49% | |=================================== | 50% | |==================================== | 51% | |==================================== | 52% | |===================================== | 53% | |====================================== | 54% | |======================================= | 55% | |======================================= | 56% | |======================================== | 57% | |========================================= | 58% | |========================================= | 59% | |========================================== | 60% | |=========================================== | 61% | |============================================ | 62% | |============================================ | 63% | |============================================= | 64% | |============================================== | 65% | |============================================== | 66% | |=============================================== | 67% | |================================================ | 68% | |================================================= | 69% | |================================================= | 70% | |================================================== | 71% | |=================================================== | 72% | |=================================================== | 73% | |==================================================== | 74% | |===================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 79% | |======================================================== | 80% | |======================================================== | 81% | |========================================================= | 82% | |========================================================== | 83% | |=========================================================== | 84% | |=========================================================== | 85% | |============================================================ | 86% | |============================================================= | 87% | |============================================================= | 88% | |============================================================== | 89% | |=============================================================== | 90% | |================================================================ | 91% | |================================================================ | 92% | |================================================================= | 93% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 97% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 100%
#R> Bootstrapping standard errors completed in 3 seconds
#R>
#R> TTa bootstrapped standard error = 0.087125125
#R>
#R> Bootstrapped confidence interval:
#R>
#R> Coef. SE [95% confidence interval]
#R> ATET (TTa) 0.07419028 0.08712513 -0.14806851 0.17499465
#R>
#R>
#R> p-value and confidence interval assuming ATET (TTa) is normally distributed:
#R>
#R> Coef. SE z P>|z| [95% confidence interval]
#R> ATET (TTa) 0.07419028 0.08712513 0.85 0.39447105 -0.09657183 0.24495238didnpreg returns a class didnp object. This object contains estimates of the average treatment effects and their standard errors. To see these, we can call the summary function.
# Print the summary of estimation
summary(tym1a)
#R> Number of Observations = 4948
#R> Number of observations in the year of the treatment and one year after the treatment = 4948
#R>
#R> Number of observations in treated group right after the treatment (N_11) = 1690
#R> Number of observations in treated group just before the treatment (N_10) = 1188
#R> Number of observations in control group right after the treatment (N_01) = 817
#R> Number of observations in control group just before the treatment (N_00) = 1253
#R>
#R> Number of Continuous Regressors = 1
#R> Number of Unordered Categorical Regressors = 1
#R> Number of Ordered Categorical Regressors = 2
#R>
#R> Bandwidths are chosen via the plug-in method
#R>
#R> Regressor Type Bandwidth
#R> 1 age ordered 9.356700e-05
#R> 2 educ ordered 9.049838e-05
#R> 3 sex factor 5.909937e-04
#R> 4 unemp continuous 2.397334e-01
#R>
#R> Unconditional Treatment Effect on the Treated (ATET):
#R>
#R> TTa = 0.07419
#R> TTa sd = 0.08713
#R> N(TTa) = 1690
#R> Bootstrapped 95% confidence interval: [-0.1481, 0.1750]
#R>
#R> p-value and confidence interval assuming ATET is normally distributed:
#R>
#R> Coef. SE z P>|z| [95% confidence interval]
#R> ATET 0.0742 0.0871 0.85 0.3945 -0.0966 0.2450
rm(tym1a)Estimating will take longer. The bandwidths are cross-validated.
# Show output as the estimation goes
tym1b <- didnpreg(
form1,
data = d0,
subset = smpl,
bwmethod = "CV",
boot.num = B,
TTx = "TTb",
print.level = 2,
digits = 4,
cores = 10)
#R> Warning in didnpreg.default(outcome = Y, regressors = X, time = time, treated =
#R> treated, : Data starts in 3, while the treatment is in 4
#R> Number of observations = 4948
#R>
#R> Number of observations in treated group after the treatment (N_ 1, 1) = 1690
#R> Number of observations in treated group before the treatment (N_ 1, 0) = 1188
#R> Number of observations in control group after the treatment (N_ 0, 1) = 817
#R> Number of observations in control group before the treatment (N_ 0, 0) = 1253
#R>
#R> Number of Continuous Regressors = 1
#R> Number of Unordered Categorical Regressors = 1
#R> Number of Ordered Categorical Regressors = 2
#R>
#R> Calculating cross-validated bandwidths
#R> Kernel Type for Continuous Regressors is Gaussian
#R> Kernel Type for Unordered Categorical Regressors is Aitchison and Aitken
#R> Kernel Type for Ordered Categorical is Li and Racine
#R> Calculating cross-validated bandwidths completed in 1 second
#R>
#R> Regressor Type Bandwidth
#R> 1 age ordered 0.10774737
#R> 2 educ ordered 0.05637391
#R> 3 sex factor 0.05638123
#R> 4 unemp continuous 0.25507958
#R>
#R> Calculating ATET: TTb
#R> TTb = 0.00269, N (TTb; all treated) = 2878
#R> Calculating ATET completed in 0 seconds
#R>
#R> Bootstrapping standard errors (99 replications)
#R> Calculating residuals completed
#R>
#R> Bootstrapping will take approximately: 5 seconds
#R>
#R> | |= | 1% | |= | 2% | |== | 3% | |=== | 4% | |==== | 5% | |==== | 6% | |===== | 7% | |====== | 8% | |====== | 9% | |======= | 10% | |======== | 11% | |========= | 12% | |========= | 13% | |========== | 14% | |=========== | 15% | |=========== | 16% | |============ | 17% | |============= | 18% | |============== | 19% | |============== | 20% | |=============== | 21% | |================ | 22% | |================ | 23% | |================= | 24% | |================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 29% | |===================== | 30% | |===================== | 31% | |====================== | 32% | |======================= | 33% | |======================== | 34% | |======================== | 35% | |========================= | 36% | |========================== | 37% | |========================== | 38% | |=========================== | 39% | |============================ | 40% | |============================= | 41% | |============================= | 42% | |============================== | 43% | |=============================== | 44% | |=============================== | 45% | |================================ | 46% | |================================= | 47% | |================================== | 48% | |================================== | 49% | |=================================== | 50% | |==================================== | 51% | |==================================== | 52% | |===================================== | 53% | |====================================== | 54% | |======================================= | 55% | |======================================= | 56% | |======================================== | 57% | |========================================= | 58% | |========================================= | 59% | |========================================== | 60% | |=========================================== | 61% | |============================================ | 62% | |============================================ | 63% | |============================================= | 64% | |============================================== | 65% | |============================================== | 66% | |=============================================== | 67% | |================================================ | 68% | |================================================= | 69% | |================================================= | 70% | |================================================== | 71% | |=================================================== | 72% | |=================================================== | 73% | |==================================================== | 74% | |===================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 79% | |======================================================== | 80% | |======================================================== | 81% | |========================================================= | 82% | |========================================================== | 83% | |=========================================================== | 84% | |=========================================================== | 85% | |============================================================ | 86% | |============================================================= | 87% | |============================================================= | 88% | |============================================================== | 89% | |=============================================================== | 90% | |================================================================ | 91% | |================================================================ | 92% | |================================================================= | 93% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 97% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 100%
#R> Bootstrapping standard errors completed in 5 seconds
#R>
#R> TTb bootstrapped standard error = 0.0796
#R>
#R> Bootstrapped confidence interval:
#R>
#R> Coef. SE [95% confidence interval]
#R> ATET (TTb) 0.0027 0.0796 -0.1049 0.2061
#R>
#R>
#R> p-value and confidence interval assuming ATET (TTb) is normally distributed:
#R>
#R> Coef. SE z P>|z| [95% confidence interval]
#R> ATET (TTb) 0.0027 0.0796 0.03 0.9730 -0.1533 0.1587Understanding [sub]samples
To work with the results for the plot,
didnpregproduces binary variables indicating different samples.
The estimation sample is captured by the esample value, which is equal to 1 if this observation was used in the estimation and 0 otherwise:
table(
d0$year[tym1b$esample],
d0$treated[tym1b$esample]
)
#R>
#R> 0 1
#R> 2010 641 490
#R> 2011 612 698
#R> 2013 490 866
#R> 2014 327 824The value sample1 indicates all treated (before and after treatment) observations in the estimation sample esample. To subset the treated observations in the original dataset, double subsetting is required.
table(
d0$year[tym1b$esample][tym1b$sample1],
d0$treated[tym1b$esample][tym1b$sample1]
)
#R>
#R> 1
#R> 2010 490
#R> 2011 698
#R> 2013 866
#R> 2014 824The value sample11 indicates the treated observations in the post-treatment period in the estimation sample esample. To subset the treated observations in the original dataset, double subsetting is required.
table(
d0$year[tym1b$esample][tym1b$sample11],
d0$treated[tym1b$esample][tym1b$sample11]
)
#R>
#R> 1
#R> 2013 866
#R> 2014 824
# or the same in case TTx = "TTa" was used by the 'didnpreg' command
table(
d0$year[tym1b$esample][tym1b$sample1][tym1b$TTa.positions.in.TTb],
d0$treated[tym1b$esample][tym1b$sample1][tym1b$TTa.positions.in.TTb]
)
#R>
#R> 1
#R> 2013 866
#R> 2014 824The values of the individual TEs can be put to the dataset using double subsetting for TTb
d0$TTbi[tym1b$esample][tym1b$sample1] <- tym1b$TTb.i
d0 %>%
group_by(year) %>%
summarize(mean = mean(TTbi, na.rm = TRUE))
#R> # A tibble: 8 × 2
#R> year mean
#R> <int> <dbl>
#R> 1 2008 NaN
#R> 2 2009 NaN
#R> 3 2010 -0.0976
#R> 4 2011 -0.110
#R> 5 2013 0.0584
#R> 6 2014 0.0995
#R> 7 2015 NaN
#R> 8 2016 NaNor TTa
d0$TTai[tym1b$esample][tym1b$sample11] <- tym1b$TTa.i
d0 %>%
group_by(year) %>%
summarize(mean = mean(TTai, na.rm = TRUE))
#R> # A tibble: 8 × 2
#R> year mean
#R> <int> <dbl>
#R> 1 2008 NaN
#R> 2 2009 NaN
#R> 3 2010 NaN
#R> 4 2011 NaN
#R> 5 2013 0.0584
#R> 6 2014 0.0995
#R> 7 2015 NaN
#R> 8 2016 NaNPlotting Heterogenous Treatment Effects
Just a remainder that TTa calculates the ATET in the post-treatment period, while TTb calculated the ATET in both prior and post-treatment periods.
To plot the heterogenous treatment effects, use the didnpplot command.
The heterogenous treatment effects can be plotted
byeither continuous or categorical variable. They can also also be plottedbyeither continuous or categorical variableoveranother categorical variable.
‘by’: factor
education
The heterogenous treatment effects are plotted for each level of education, since the education is a categorical variable.
tym1b_gr_educ <- didnpplot(
obj = tym1b,
level = 90,
by = d0$educ[tym1b$esample][tym1b$sample1],
xlab = "Education",
ylab = "ATET"
)
#R> [1] "1. 'by' is catergorical"
#R> [1] "1.1 TTa + TTb"
#R> [1] "1.1.1.1 TTb"
# A
tym1b_gr_educ$data.a
#R> atet atet.sd count by
#R> 1 0.10792531 0.10360520 315 7
#R> 2 0.08590395 0.07209783 1099 6
#R> 3 -0.01155122 0.16378588 146 8
#R> 4 0.09638786 0.15952821 108 10
#R> 5 -0.20622072 0.14607889 22 11
tym1b_gr_educ$plot.a
# B
tym1b_gr_educ$data.b
#R> atet atet.sd count by
#R> 1 -0.013384275 0.11395764 544 7
#R> 2 -0.004822337 0.09689843 1911 6
#R> 3 0.025177550 0.14252837 201 8
#R> 4 0.139390533 0.16681813 187 10
#R> 5 -0.196831130 0.15695523 35 11
tym1b_gr_educ$plot.b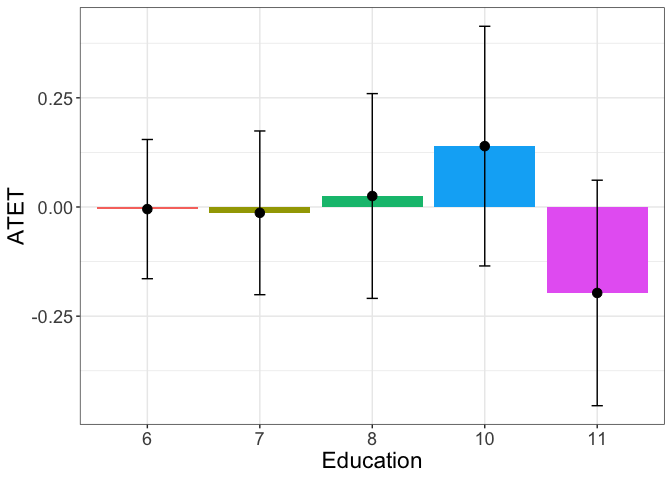
# ggsave(paste0("atet_ci_education.pdf"), width = 15, height = 10, units = c("cm"))Here objects data.a and data.b contain data that is used to produce plot.a and plot.b. The graphs are ggplot objects and can be amended further.
time
The heterogenous treatment effects over time show that the effect is significant in the second year after the treatment.
Note that the graph shows the 90% confidence interval bygiving the option
level = 90.
tym1b_gr_time <- didnpplot(
obj = tym1b,
level = 90,
by = factor(d0$t)[tym1b$esample][tym1b$sample1],
by.labels.values = data.frame(c("-1","0","1","2"), c("2010", "2011", "2013", "2014")),
xlab = "Year",
ylab = "ATET"
)
#R> [1] "1. 'by' is catergorical"
#R> [1] "1.1 TTa + TTb"
#R> [1] "1.1.1.1 TTb"
# A
tym1b_gr_time$data.a
#R> atet atet.sd count by byold
#R> 1 NaN NA 0 2010 -1
#R> 2 NaN NA 0 2011 0
#R> 3 0.05840563 0.05889966 866 2013 1
#R> 4 0.09952936 0.07018234 824 2014 2
tym1b_gr_time$plot.a
#R> Warning: Removed 2 rows containing missing values or values outside the scale range
#R> (`geom_bar()`).
#R> Warning: Removed 2 rows containing missing values or values outside the scale range
#R> (`geom_point()`).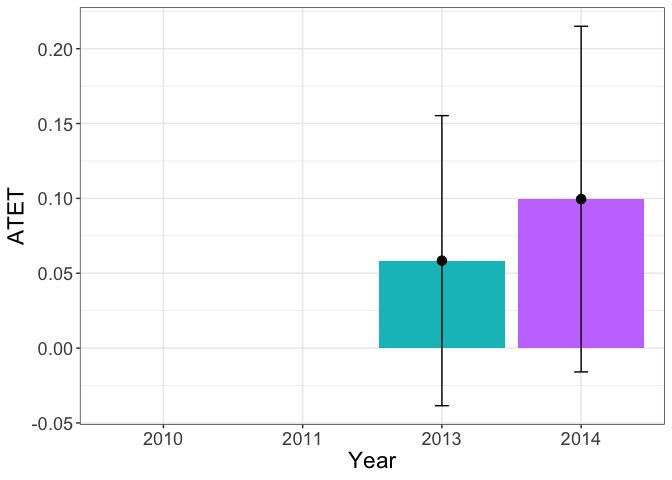
# B
tym1b_gr_time$data.b
#R> atet atet.sd count by byold
#R> 1 -0.09763422 0.17194937 490 2010 -1
#R> 2 -0.11032894 0.14665580 698 2011 0
#R> 3 0.05840563 0.05889966 866 2013 1
#R> 4 0.09952936 0.07018234 824 2014 2
tym1b_gr_time$plot.b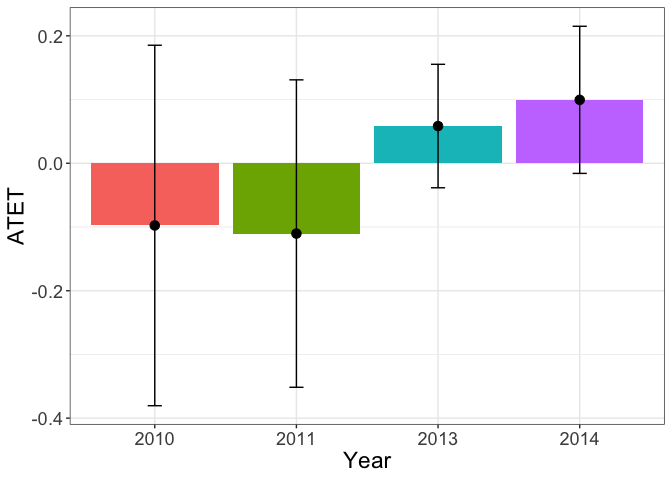
# ggsave(paste0("atet_ci_time.pdf"), width = 15, height = 10, units = c("cm"))sex
Another example is the graph with the heterogenous treatment effects by sex:
tym1b_gr_sex <- didnpplot(
obj = tym1b,
level = 90,
by = d0$sex[tym1b$esample][tym1b$sample1],
xlab = "Sex",
ylab = "ATET",
by.labels.values = data.frame(c("1","2"), c("Male", "Female"))
)
#R> [1] "1. 'by' is catergorical"
#R> [1] "1.1 TTa + TTb"
#R> [1] "1.1.1.1 TTb"
# A
tym1b_gr_sex$data.a
#R> atet atet.sd count by byold
#R> 1 0.13263322 0.07018602 830 Male 1
#R> 2 0.02616964 0.08545339 860 Female 2
tym1b_gr_sex$plot.a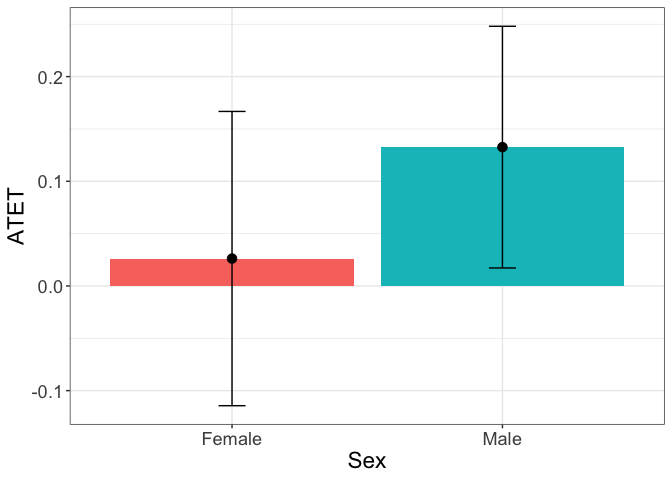
# B
tym1b_gr_sex$data.b
#R> atet atet.sd count by byold
#R> 1 0.09857137 0.10754282 1440 Male 1
#R> 2 -0.09332522 0.08357793 1438 Female 2
tym1b_gr_sex$plot.b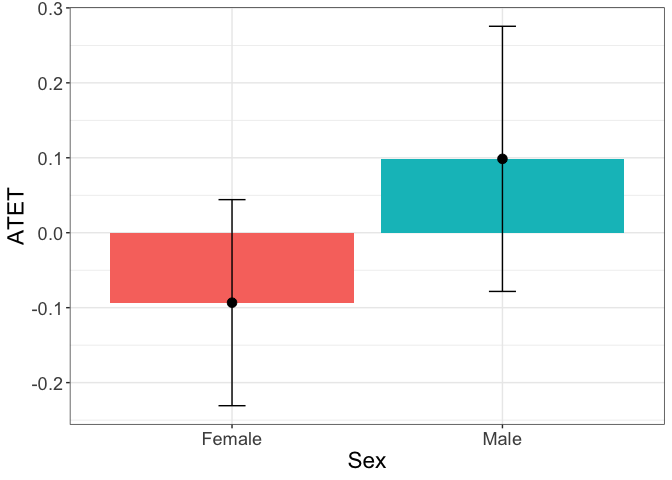
# ggsave(paste0("atet_ci_sex.pdf"), width = 15, height = 10, units = c("cm"))‘by’ continuous: unemp
When the ‘by’ variable is continuous (the didnpplot command will recognize if by is a continuous variable) the didnpplot offers three ways of plotting the heterogeneous treatment effects.
Scale of the continuous ‘by’ is its range
If by.continuous.scale is not specified, didnpplot will use each unique value in the by variable to produce the plot, which can be pretty rugged.
tym1b_gr_unemp_each_value <- didnpplot(
obj = tym1b,
level = 90,
by = d0$unemp[tym1b$esample][tym1b$sample1],
xlab = "Unemployment",
ylab = "ATET",
add.zero.line = FALSE
)
#R> [1] "2. 'by' is continuous"
#R> [1] "Scale of the continuous 'by' is its range"
#R> [1] "2.1 TTa + TTb"
#R> [1] "2.1.1 only 'by'"
#R> [1] "2.1.1.1 TTb"
#R> [1] "2.1.1.2 TTa"
# A
head(tym1b_gr_unemp_each_value$data.a, 10)
#R> by atet atet.sd count bySorted
#R> 1 3.250000 -0.116735486 0.1730414 5 11
#R> 2 3.633333 0.244916417 0.1391599 12 12
#R> 3 3.675000 -0.163110524 0.1857630 2 13
#R> 4 4.208333 -0.008850374 0.1380482 8 14
#R> 5 4.225000 0.021161353 0.1588585 2 15
#R> 6 4.266667 0.352318401 0.1378871 3 16
#R> 7 4.333333 -0.082006287 0.2486211 2 17
#R> 8 4.341667 0.265753703 0.1448199 2 18
#R> 9 4.383333 0.478780569 0.1678811 2 19
#R> 10 4.508333 0.347497049 0.1274053 4 20
tym1b_gr_unemp_each_value$plot.a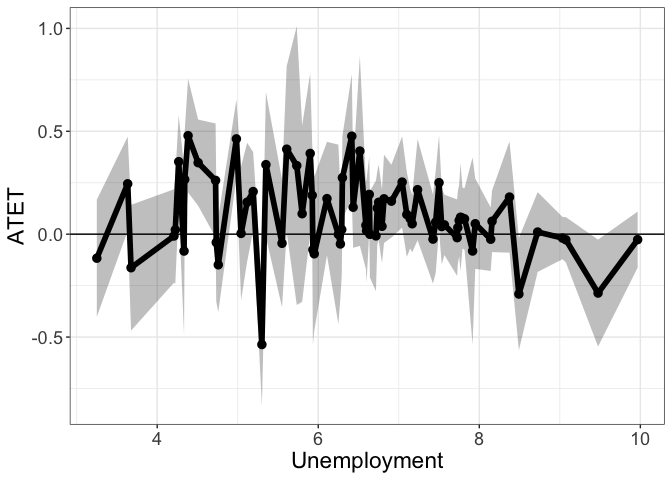
# B
head(tym1b_gr_unemp_each_value$data.b, 10)
#R> by atet atet.sd count bySorted
#R> 90 8.358333 0.0001284317 0.10936676 6 100
#R> 91 8.375000 0.1804007431 0.16428889 4 101
#R> 92 8.491667 -0.2909395634 0.16592609 1 102
#R> 93 8.525000 -0.1996837095 0.09767867 13 103
#R> 94 8.641667 0.6499037291 0.32873993 1 104
#R> 95 8.658333 -0.2872246202 0.28476744 1 105
#R> 96 8.691667 -0.0228657597 0.08704620 15 106
#R> 97 8.716667 -0.1457732130 0.12718286 2 107
#R> 98 8.725000 0.0103503330 0.11788690 3 108
#R> 99 8.758333 -0.3328329294 0.15271056 2 109
tym1b_gr_unemp_each_value$plot.b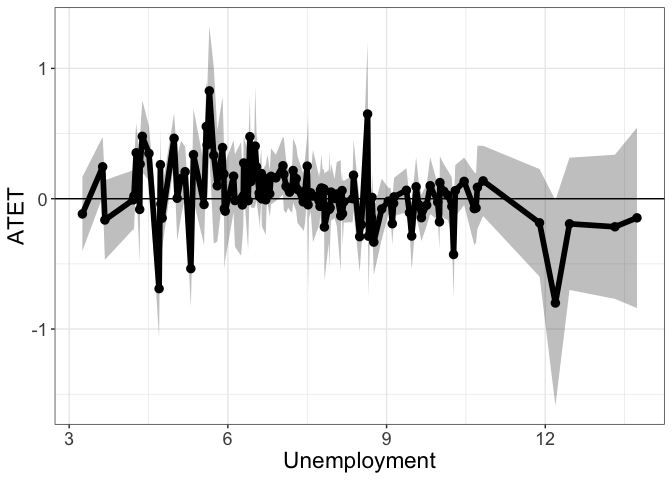
# ggsave(paste0("atet_ci_unemp_numeric.pdf"), width = 15, height = 10, units = c("cm"))Ameding a ggplot object is easy. For example adding a 0 horizontal line is
tym1b_gr_unemp_each_value$plot.a +
geom_hline(yintercept = 0)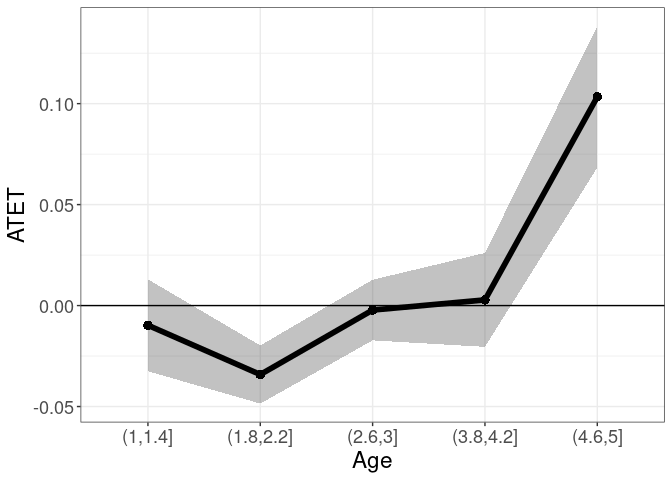
Anternatively, one can use the
data.aanddata.bobjects to plot from scratch.
Scale of the continuous ‘by’ intervals
Setting by.continuous.scale to a single number, instructs didnpplot to split the range of the continuous by variable into the number of intervals specified by by.continuous.scale and plot ATET by intervals.
tym1b_gr_unemp_n_intervals <- didnpplot(
obj = tym1b,
level = 90,
by = d0$unemp[tym1b$esample][tym1b$sample1],
by.continuous.scale = 10,
xaxis.label.angle = 90,
xlab = "Unemployment",
ylab = "ATET",
by.labels.values = data.frame(c("1","2"), c("Male", "Female"))
)
#R> [1] "2. 'by' is continuous"
#R> [1] "Scale of the continuous 'by' is determined by the number of intervals 'by.continuous.scale'"
#R> [1] "2.1 TTa + TTb"
#R> [1] "2.1.1 only 'by'"
#R> [1] "2.1.1.1 TTb"
#R> [1] "2.1.1.2 TTa"
# A
tym1b_gr_unemp_n_intervals$data.a
#R> by atet atet.sd count bySorted
#R> 1 (3.24,3.92] 0.10679466 0.13742108 19 11
#R> 2 (3.92,4.59] 0.16276170 0.10615043 23 12
#R> 3 (4.59,5.27] 0.21783610 0.11400609 183 13
#R> 4 (5.27,5.94] 0.15026060 0.14598266 31 14
#R> 5 (5.94,6.61] 0.22523441 0.11723207 235 15
#R> 6 (6.61,7.28] 0.08989266 0.08594099 155 16
#R> 7 (7.28,7.95] 0.04889052 0.08833423 497 17
#R> 8 (7.95,8.62] 0.04050111 0.08335645 38 18
#R> 9 (8.62,9.3] -0.01945809 0.06259306 475 19
#R> 10 (9.3,9.97] -0.03416828 0.08323956 34 20
tym1b_gr_unemp_n_intervals$plot.a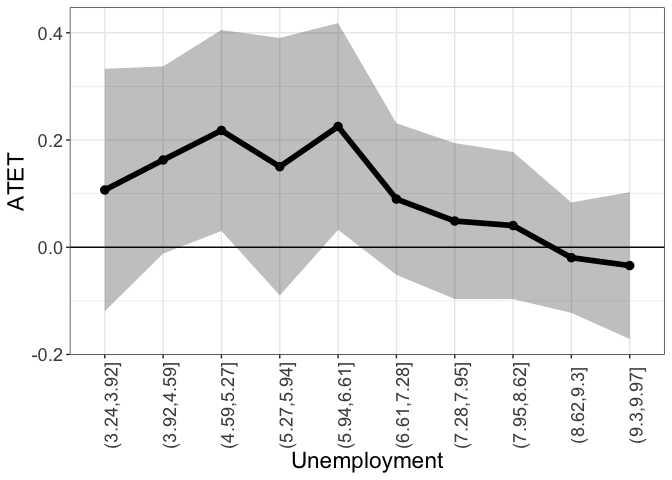
# B
tym1b_gr_unemp_n_intervals$data.b
#R> by atet atet.sd count bySorted
#R> 4 (3.24,4.3] 0.095549170 0.11519134 32 11
#R> 5 (4.3,5.35] 0.208246917 0.11170587 196 12
#R> 6 (5.35,6.39] 0.242905084 0.12155989 233 13
#R> 7 (6.39,7.44] 0.101167850 0.08528435 218 14
#R> 8 (7.44,8.49] 0.028286072 0.08494846 805 15
#R> 9 (8.49,9.54] -0.031809629 0.06191695 577 16
#R> 10 (9.54,10.6] 0.007166155 0.08511938 146 17
#R> 1 (10.6,11.6] 0.026221646 0.15061713 31 18
#R> 2 (11.6,12.7] -0.188963523 0.27263386 612 19
#R> 3 (12.7,13.7] -0.193354811 0.35653591 28 20
tym1b_gr_unemp_n_intervals$plot.b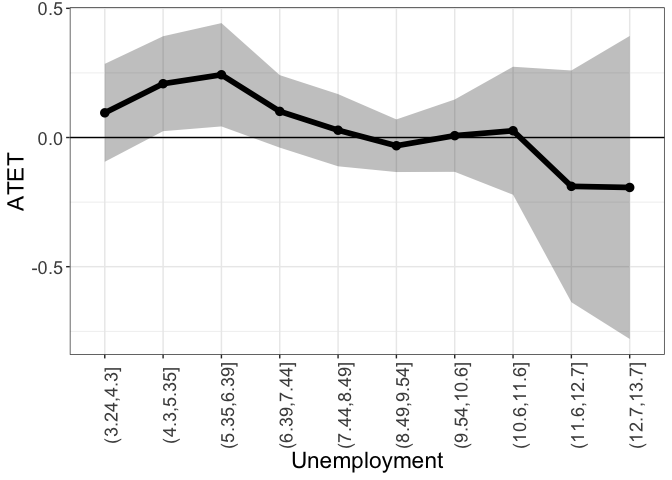
# ggsave(paste0("atet_ci_unemp_intervals.pdf"), width = 15, height = 10, units = c("cm"))Scale of the continuous ‘by’ a vector
Setting by.continuous.scale to a single number, instructs didnpplot to split the range of the continuous by variable into intervals defined by the specified vector and plot ATET by intervals.
tym1b_gr_unemp_vector_breaks <- didnpplot(
obj = tym1b,
level = 90,
by = d0$unemp[tym1b$esample][tym1b$sample1],
by.continuous.scale = c(2, 3, 4, 5, 7, 9, 12),
xlab = "Unemployment",
ylab = "ATET",
by.labels.values = data.frame(c("1","2"), c("Male", "Female"))
)
#R> [1] "2. 'by' is continuous"
#R> [1] "Scale of the continuous 'by' is determined by the vector in 'by.continuous.scale'"
#R> [1] "2.1 TTa + TTb"
#R> [1] "2.1.1 only 'by'"
#R> [1] "2.1.1.1 TTb"
#R> [1] "2.1.1.2 TTa"
# A
tym1b_gr_unemp_vector_breaks$data.a
#R> by atet atet.sd count bySorted
#R> 5 [3.25,4] 0.10679466 0.13742108 19 11
#R> 1 (4,5] 0.24313543 0.09729941 42 12
#R> 2 (5,7] 0.19543022 0.10141037 512 13
#R> 3 (7,9] 0.05028768 0.08603009 611 14
#R> 4 (9,9.97] -0.02062325 0.06195741 506 15
tym1b_gr_unemp_vector_breaks$plot.a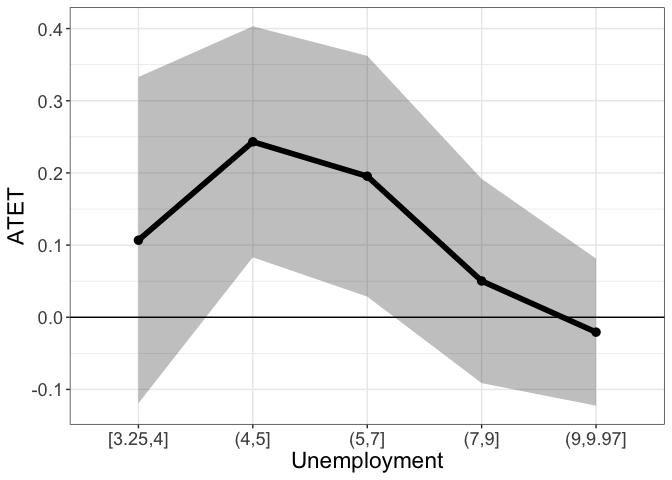
# B
tym1b_gr_unemp_vector_breaks$data.b
#R> by atet atet.sd count bySorted
#R> 6 [3.25,4] 0.10679466 0.13742108 19 11
#R> 2 (4,5] 0.22143408 0.09725556 43 12
#R> 3 (5,7] 0.19881192 0.10147109 525 13
#R> 4 (7,9] 0.02712679 0.08311250 937 14
#R> 5 (9,12] -0.07482362 0.10357186 1085 15
#R> 1 (12,13.7] -0.19487026 0.31170720 269 16
tym1b_gr_unemp_vector_breaks$plot.b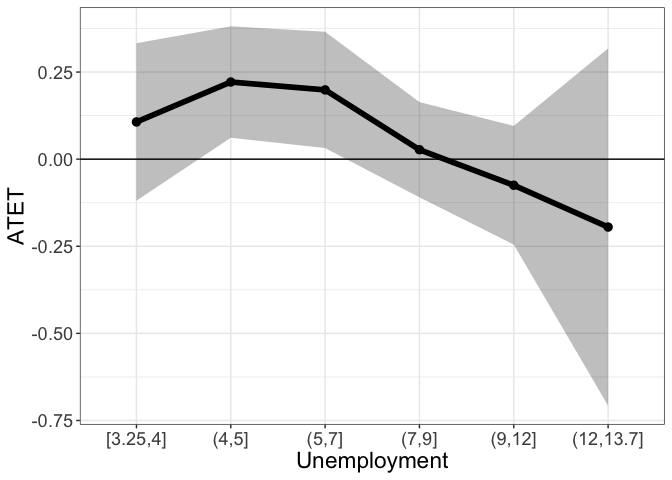
# ggsave(paste0("atet_ci_unemp_breaks.pdf"), width = 15, height = 10, units = c("cm"))‘by’: factor + ’over
The heterogeneous treatment effects can be plotted by either a continuous or categorical variable over a categorical variable.
‘by’: sex; ‘over’ is time
This is an example with treatment effects by sex over time.
tym1b_gr_sex_time <- didnpplot(
obj = tym1b,
level = 90,
by = d0$sex[tym1b$esample][tym1b$sample1],
over = as.factor( d0$t[tym1b$esample][tym1b$sample1]),
# over = d0$educ[tym1b$esample][tym1b$sample1],
xlab = "Sex",
ylab = "ATET",
by.labels.values = data.frame(c("1","2"), c("Male", "Female")),
over.labels.values = data.frame(c("-1","0","1","2"), c("2010", "2011", "2013", "2014")),
)
#R> [1] "1. 'by' is catergorical"
#R> [1] "1.1 TTa + TTb"
#R> [1] "1.1.2 'by' + 'over'"
# A
tym1b_gr_sex_time$data.a
#R> atet atet.sd count by byold over overold overSorted
#R> 1 0.16122300 0.06998495 435 Male 1 2013 1 13
#R> 2 -0.04536597 0.08490582 431 Female 2 2013 1 13
#R> 3 0.10114827 0.08466214 395 Male 1 2014 2 14
#R> 4 0.09803875 0.09676866 429 Female 2 2014 2 14
tym1b_gr_sex_time$plot.a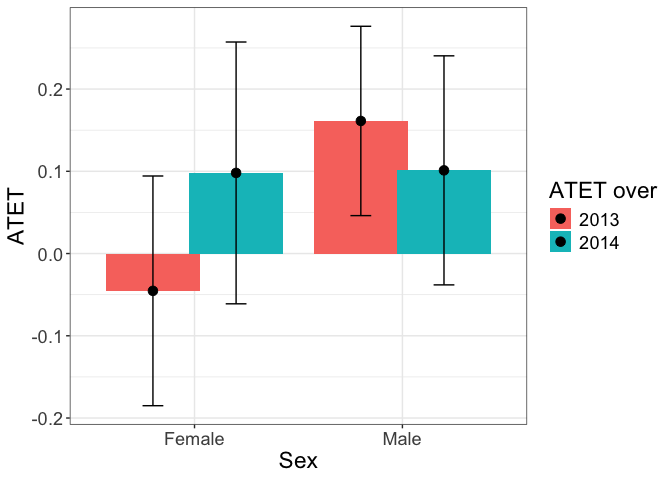
# B
tym1b_gr_sex_time$data.b
#R> atet atet.sd count by byold over overold overSorted bySorted
#R> 2 -0.28086872 0.15917328 233 Female 2 2010 -1 11 11
#R> 1 0.06848888 0.22402857 257 Male 1 2010 -1 11 12
#R> 4 -0.26453668 0.13076795 345 Female 2 2011 0 12 11
#R> 3 0.04038400 0.20358962 353 Male 1 2011 0 12 12
#R> 6 -0.04536597 0.08490582 431 Female 2 2013 1 13 11
#R> 5 0.16122300 0.06998495 435 Male 1 2013 1 13 12
#R> 8 0.09803875 0.09676866 429 Female 2 2014 2 14 11
#R> 7 0.10114827 0.08466214 395 Male 1 2014 2 14 12
tym1b_gr_sex_time$plot.b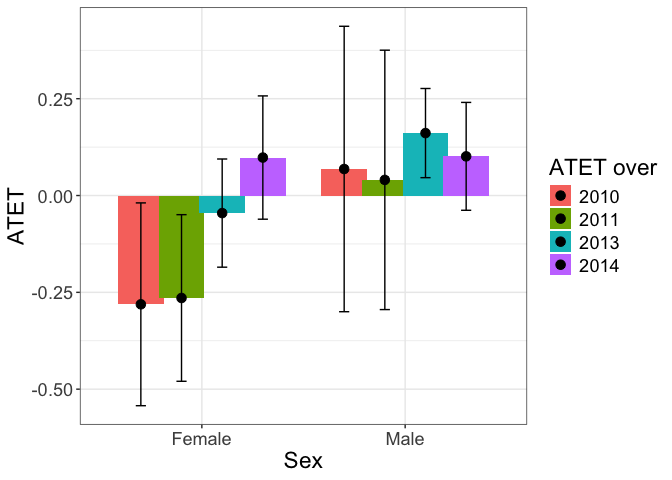
# ggsave(paste0("atet_ci_sex_time.pdf"), width = 15, height = 10, units = c("cm"))‘by’: time; ‘over’ is sex
This is an example with treatment effects by time over sex, reversing the order of the previous graph.
tym1b_gr_time_sex <- didnpplot(
obj = tym1b,
level = 90,
over = d0$sex[tym1b$esample][tym1b$sample1],
by = as.factor( d0$t[tym1b$esample][tym1b$sample1]),
xlab = "Year",
ylab = "ATET",
by.labels.values = data.frame(c("-1","0","1","2"), c("2010", "2011", "2013", "2014")),
over.labels.values = data.frame(c("1","2"), c("Male", "Female"))
)
#R> [1] "1. 'by' is catergorical"
#R> [1] "1.1 TTa + TTb"
#R> [1] "1.1.2 'by' + 'over'"
# A
tym1b_gr_time_sex$data.a
#R> atet atet.sd count by byold over overold overSorted
#R> 1 0.16122300 0.06998495 435 2013 1 Male 1 11
#R> 2 0.10114827 0.08466214 395 2014 2 Male 1 11
#R> 3 -0.04536597 0.08490582 431 2013 1 Female 2 12
#R> 4 0.09803875 0.09676866 429 2014 2 Female 2 12
tym1b_gr_time_sex$plot.a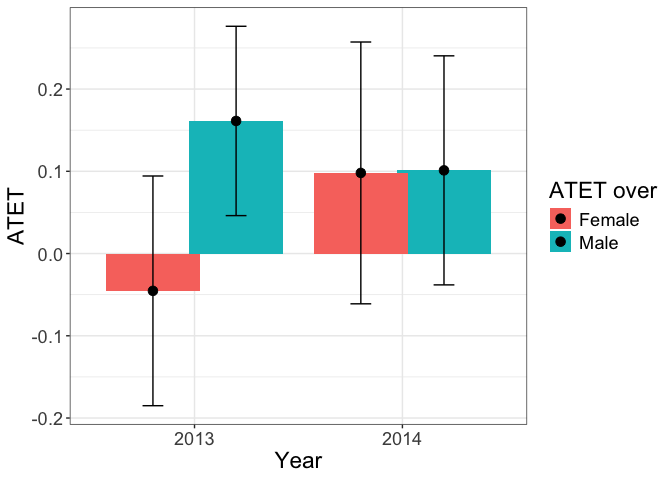
# B
tym1b_gr_time_sex$data.b
#R> atet atet.sd count by byold over overold overSorted bySorted
#R> 1 0.06848888 0.22402857 257 2010 -1 Male 1 11 11
#R> 2 0.04038400 0.20358962 353 2011 0 Male 1 11 12
#R> 3 0.16122300 0.06998495 435 2013 1 Male 1 11 13
#R> 4 0.10114827 0.08466214 395 2014 2 Male 1 11 14
#R> 5 -0.28086872 0.15917328 233 2010 -1 Female 2 12 11
#R> 6 -0.26453668 0.13076795 345 2011 0 Female 2 12 12
#R> 7 -0.04536597 0.08490582 431 2013 1 Female 2 12 13
#R> 8 0.09803875 0.09676866 429 2014 2 Female 2 12 14
tym1b_gr_time_sex$plot.b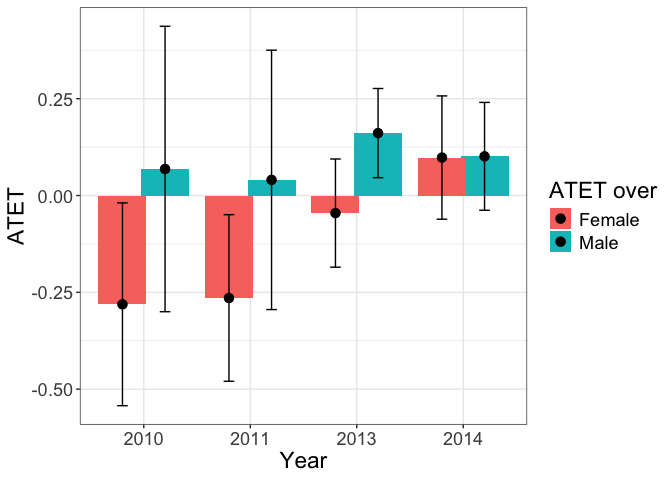
# ggsave(paste0("atet_ci_time_sex.pdf"), width = 15, height = 10, units = c("cm"))Alternatively use the data from the object
tym1b_gr_time_sex
to produce another type of graph:
crit.value <- 2
pd <- position_dodge(0.1) # move them .05 to the left and right
d1 <- tym1b_gr_time_sex$data.b
d1$Sex <- d1$over
ggplot(d1, aes(x = by, y = atet, color = Sex, group = Sex)) +
geom_errorbar(aes(ymin = atet - crit.value*atet.sd, ymax = atet + crit.value*atet.sd), color = "black", width = .1, position = pd) +
geom_line(position = pd) +
geom_point(position = pd, size = 3, shape = 21, fill = "white") +
xlab("Time") +
ylab("ATET") +
theme_bw() +
theme(legend.position = "right", text = element_text(size = 17))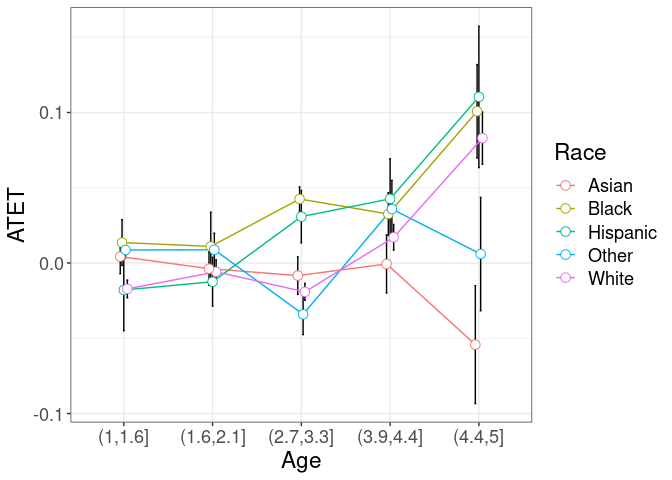
‘by’ continuous: unemp + ‘over’
The following examples use continuous by variable to plot the heterogeneous treatment effects over sex.
Scale of the continuous ‘by’ is its range
by.continuous.scale is not specified or NULL.
tym1b_gr_unemp_each_value_sex <- didnpplot(
obj = tym1b,
level = 90,
by = d0$unemp[tym1b$esample][tym1b$sample1],
over = d0$sex[tym1b$esample][tym1b$sample1],
xlab = "Unemployment",
ylab = "ATET",
over.labels.values = data.frame(c("1","2"), c("Male", "Female"))
)
#R> [1] "2. 'by' is continuous"
#R> [1] "Scale of the continuous 'by' is its range"
#R> [1] "2.1 TTa + TTb"
#R> [1] "2.1.2 'by' + 'over'"
#R> [1] "2.1.2.1 TTb"
#R> [1] "2.1.2.2 TTa"
# A
head(tym1b_gr_unemp_each_value_sex$data.a)
#R> atet atet.sd count by over overold bySorted
#R> 1 0.1335883 0.2119510 3 3.250000 Male 1 11
#R> 68 -0.4922212 0.2495373 2 3.250000 Female 2 11
#R> 3 0.1404041 0.1695159 8 3.633333 Male 1 12
#R> 70 0.4539411 0.1701409 4 3.633333 Female 2 12
#R> 111 -0.1631105 0.1857630 2 3.675000 Female 2 13
#R> 6 -0.5463821 0.2344738 3 4.208333 Male 1 14
tym1b_gr_unemp_each_value_sex$plot.a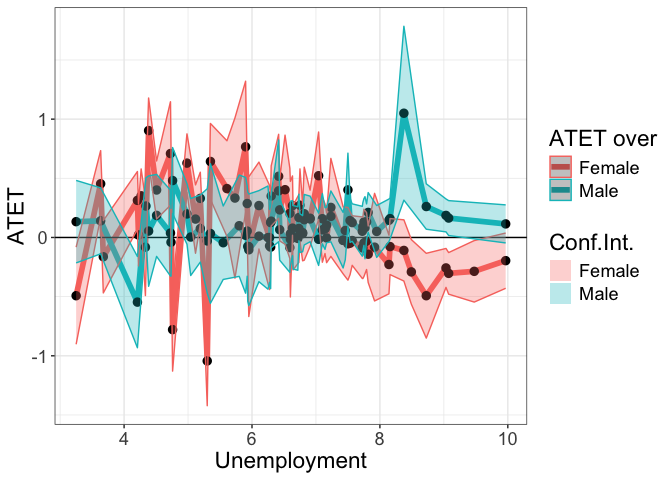
# B
head(tym1b_gr_unemp_each_value_sex$data.b)
#R> atet atet.sd count by over overold bySorted
#R> 1 0.08142841 0.1395427 4 8.358333 Male 1 100
#R> 134 -0.16247152 0.2084496 2 8.358333 Female 2 100
#R> 3 1.05007326 0.4467315 1 8.375000 Male 1 101
#R> 136 -0.10949010 0.1572680 3 8.375000 Female 2 101
#R> 109 -0.29093956 0.1659261 1 8.491667 Female 2 102
#R> 6 0.15073181 0.1084040 2 8.525000 Male 1 103
tym1b_gr_unemp_each_value_sex$plot.b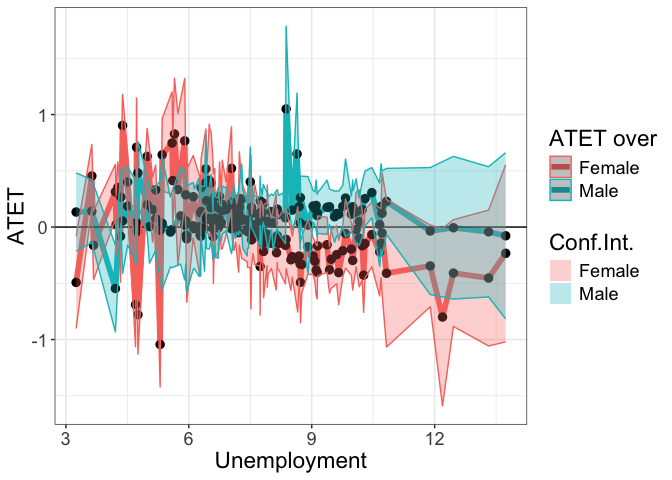
# ggsave(paste0("atet_ci_unemp_sex_numeric.pdf"), width = 15, height = 10, units = c("cm"))Scale of the continuous ‘by’ intervals
by.continuous.scale is a scalar.
tym1b_gr_unemp_intervals_sex <- didnpplot(
obj = tym1b,
level = 90,
by = d0$unemp[tym1b$esample][tym1b$sample1],
by.continuous.scale = 15,
xaxis.label.angle = 90,
over = d0$sex[tym1b$esample][tym1b$sample1],
xlab = "Unemployment",
ylab = "ATET",
over.labels.values = data.frame(c("1","2"), c("Male", "Female"))
)
#R> [1] "2. 'by' is continuous"
#R> [1] "Scale of the continuous 'by' is determined by the number of intervals 'by.continuous.scale'"
#R> [1] "2.1 TTa + TTb"
#R> [1] "2.1.2 'by' + 'over'"
#R> [1] "2.1.2.1 TTb"
#R> [1] "2.1.2.2 TTa"
# A
tym1b_gr_unemp_intervals_sex$data.a
#R> atet atet.sd count by over overold bySorted
#R> 1 0.13854523 0.17418488 11 (3.24,3.7] Male 1 11
#R> 15 0.06313763 0.16342893 8 (3.24,3.7] Female 2 11
#R> 2 -0.12389278 0.15962855 7 (4.15,4.59] Male 1 13
#R> 16 0.28817303 0.11967339 16 (4.15,4.59] Female 2 13
#R> 3 0.16775941 0.15247430 9 (4.59,5.04] Male 1 14
#R> 17 0.49583342 0.13514583 10 (4.59,5.04] Female 2 14
#R> 4 0.07191305 0.17439950 81 (5.04,5.49] Male 1 15
#R> 18 0.31234619 0.13182851 87 (5.04,5.49] Female 2 15
#R> 5 0.02971840 0.22015522 13 (5.49,5.94] Male 1 16
#R> 19 0.33346430 0.16649108 14 (5.49,5.94] Female 2 16
#R> 6 0.10131513 0.14462815 75 (5.94,6.38] Male 1 17
#R> 20 0.32993938 0.15069689 122 (5.94,6.38] Female 2 17
#R> 7 0.06300613 0.11079547 52 (6.38,6.83] Male 1 18
#R> 21 0.15992589 0.13896489 60 (6.38,6.83] Female 2 18
#R> 8 0.10386199 0.09200865 40 (6.83,7.28] Male 1 19
#R> 22 0.04843555 0.12207732 41 (6.83,7.28] Female 2 19
#R> 9 0.12714149 0.09586106 199 (7.28,7.73] Male 1 20
#R> 23 -0.02703933 0.12796298 224 (7.28,7.73] Female 2 20
#R> 10 0.16055074 0.09740943 66 (7.73,8.18] Male 1 21
#R> 24 -0.10813962 0.12899924 41 (7.73,8.18] Female 2 21
#R> 11 1.05007326 0.44673151 1 (8.18,8.62] Male 1 22
#R> 25 -0.15485246 0.14147183 4 (8.18,8.62] Female 2 22
#R> 12 0.18707317 0.08462696 232 (8.62,9.07] Male 1 23
#R> 26 -0.25853150 0.09984337 199 (8.62,9.07] Female 2 23
#R> 13 0.16406398 0.08962362 26 (9.07,9.52] Male 1 24
#R> 27 -0.30250744 0.10623489 19 (9.07,9.52] Female 2 24
#R> 14 0.11466916 0.09779138 18 (9.52,9.97] Male 1 25
#R> 28 -0.19597262 0.14204376 15 (9.52,9.97] Female 2 25
tym1b_gr_unemp_intervals_sex$plot.a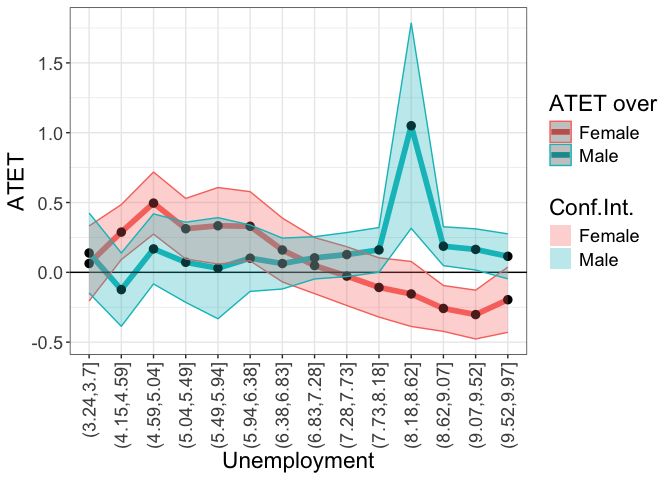
# B
tym1b_gr_unemp_intervals_sex$data.b
#R> atet atet.sd count by over overold bySorted
#R> 1 0.13854523 0.17418488 11 (3.24,3.95] Male 1 11
#R> 15 0.06313763 0.16342893 8 (3.24,3.95] Female 2 11
#R> 2 -0.12389278 0.15962855 7 (3.95,4.65] Male 1 12
#R> 16 0.28817303 0.11967339 16 (3.95,4.65] Female 2 12
#R> 3 0.08203792 0.16792176 89 (4.65,5.35] Male 1 13
#R> 17 0.31752554 0.12976499 97 (4.65,5.35] Female 2 13
#R> 4 0.01106405 0.21509676 17 (5.35,6.05] Male 1 14
#R> 18 0.41503084 0.16648173 20 (5.35,6.05] Female 2 14
#R> 5 0.09112630 0.13355624 116 (6.05,6.74] Male 1 15
#R> 19 0.29934171 0.14764786 161 (6.05,6.74] Female 2 15
#R> 6 0.09355733 0.08469647 63 (6.74,7.44] Male 1 16
#R> 20 0.07437828 0.12651839 74 (6.74,7.44] Female 2 16
#R> 7 0.13546254 0.09225585 329 (7.44,8.14] Male 1 17
#R> 21 -0.06344739 0.12461916 333 (7.44,8.14] Female 2 17
#R> 8 0.14549336 0.09632050 84 (8.14,8.84] Male 1 18
#R> 22 -0.17199636 0.12251963 97 (8.14,8.84] Female 2 18
#R> 9 0.17998778 0.08470152 292 (8.84,9.54] Male 1 19
#R> 23 -0.27172992 0.09843304 247 (8.84,9.54] Female 2 19
#R> 10 0.12593461 0.09318934 50 (9.54,10.2] Male 1 20
#R> 24 -0.21417580 0.13970175 46 (9.54,10.2] Female 2 20
#R> 11 0.22553765 0.14910030 45 (10.2,10.9] Male 1 21
#R> 25 -0.13151966 0.17163645 36 (10.2,10.9] Female 2 21
#R> 12 -0.03548073 0.34293848 192 (11.6,12.3] Male 1 23
#R> 26 -0.34792833 0.22087235 180 (11.6,12.3] Female 2 23
#R> 13 -0.00614826 0.38551391 129 (12.3,13] Male 1 24
#R> 27 -0.40912748 0.28862963 111 (12.3,13] Female 2 24
#R> 14 -0.05335951 0.37246881 16 (13,13.7] Male 1 25
#R> 28 -0.38001521 0.38901319 12 (13,13.7] Female 2 25
tym1b_gr_unemp_intervals_sex$plot.b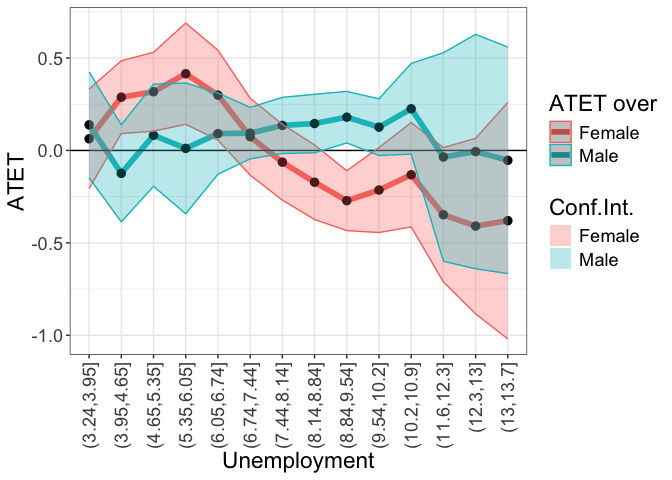
# ggsave(paste0("atet_ci_unemp_sex_intervals.pdf"), width = 15, height = 10, units = c("cm"))Scale of the continuous ‘by’ a vector
by.continuous.scale is a vector. Note even if the user provides an interval wider than the range of the continuous by variable didnpplot will take care of that and define the plausible range for plotting. In this example, print.level = 2 option is used to show the working of the didnpplot command.
tym1b_gr_unemp_breaks_sex <- didnpplot(
obj = tym1b,
level = 90,
by = d0$unemp[tym1b$esample][tym1b$sample1],
by.continuous.scale = seq(0, 15, 1), #c(2, 5, 7, 9, 12),
over = d0$sex[tym1b$esample][tym1b$sample1],
xlab = "Unemployment",
ylab = "ATET",
over.labels.values = data.frame(c("1","2"), c("Male", "Female")),
print.level = 2
)
#R> [1] "Female" "Male"
#R> over.over.levels:
#R> over overnew overSorted
#R> 1 1 Male 11
#R> 2 2 Female 12
#R> [1] "2. 'by' is continuous"
#R> [1] "Scale of the continuous 'by' is determined by the vector in 'by.continuous.scale'"
#R> by bySorted
#R> 1 [3.25,4] 11
#R> 2 (4,5] 12
#R> 3 (5,6] 13
#R> 4 (6,7] 14
#R> 5 (7,8] 15
#R> 6 (8,9] 16
#R> 7 (9,10] 17
#R> 8 (10,11] 18
#R> 9 (11,12] 19
#R> 10 (12,13] 20
#R> 11 (13,13.7] 21
#R> [1] "2.1 TTa + TTb"
#R> [1] "2.1.2 'by' + 'over'"
#R> [1] "2.1.2.1 TTb"
#R> d1b:
#R> atet atet.sd count by over overold bySorted
#R> 1 0.13854523 0.17418488 11 [3.25,4] Male 1 11
#R> 12 0.06313763 0.16342893 8 [3.25,4] Female 2 11
#R> 2 0.04016158 0.14429305 16 (4,5] Male 1 12
#R> 13 0.32885483 0.11108723 27 (4,5] Female 2 12
#R> 3 0.06164566 0.17819887 97 (5,6] Male 1 13
#R> 14 0.32860643 0.13221780 106 (5,6] Female 2 13
#R> 4 0.08969653 0.12484310 134 (6,7] Male 1 14
#R> 15 0.27417561 0.14359173 188 (6,7] Female 2 14
#R> 5 0.12961801 0.09338113 295 (7,8] Male 1 15
#R> 16 -0.02620078 0.12531064 307 (7,8] Female 2 15
#R> 6 0.14033220 0.09453717 164 (8,9] Male 1 16
#R> 17 -0.16251668 0.12633197 171 (8,9] Female 2 16
#R> 7 0.17531574 0.08320480 330 (9,10] Male 1 17
#R> 18 -0.26574815 0.09987550 286 (9,10] Female 2 17
#R> 8 0.19875742 0.13870169 56 (10,11] Male 1 18
#R> 19 -0.13154181 0.16909861 42 (10,11] Female 2 18
#R> 9 -0.03548073 0.34293848 192 (11,12] Male 1 19
#R> 20 -0.34540341 0.22072871 179 (11,12] Female 2 19
#R> 10 -0.00614826 0.38551391 129 (12,13] Male 1 20
#R> 21 -0.41261642 0.28848880 112 (12,13] Female 2 20
#R> 11 -0.05335951 0.37246881 16 (13,13.7] Male 1 21
#R> 22 -0.38001521 0.38901319 12 (13,13.7] Female 2 21
#R> d1b2:
#R> by bySorted
#R> 1 [3.25,4] 11
#R> 2 (4,5] 12
#R> 3 (5,6] 13
#R> 4 (6,7] 14
#R> 5 (7,8] 15
#R> 6 (8,9] 16
#R> 7 (9,10] 17
#R> 8 (10,11] 18
#R> 9 (11,12] 19
#R> 10 (12,13] 20
#R> 11 (13,13.7] 21
#R> [1] "2.1.2.2 TTa"
#R> by bySorted
#R> 1 [3.25,4] 11
#R> 2 (4,5] 12
#R> 3 (5,6] 13
#R> 4 (6,7] 14
#R> 5 (7,8] 15
#R> 6 (8,9] 16
#R> 7 (9,9.97] 17
#R> d1a:
#R> atet atet.sd count by over overold bySorted
#R> 1 0.13854523 0.17418488 11 [3.25,4] Male 1 11
#R> 8 0.06313763 0.16342893 8 [3.25,4] Female 2 11
#R> 2 0.04016158 0.14429305 16 (4,5] Male 1 12
#R> 9 0.36804241 0.11160670 26 (4,5] Female 2 12
#R> 3 0.06252843 0.17917111 96 (5,6] Male 1 13
#R> 10 0.31142244 0.13154404 102 (5,6] Female 2 13
#R> 4 0.09026293 0.12570475 128 (6,7] Male 1 14
#R> 11 0.27278924 0.14304280 186 (6,7] Female 2 14
#R> 5 0.12946909 0.09386141 283 (7,8] Male 1 15
#R> 12 -0.02607691 0.12604353 287 (7,8] Female 2 15
#R> 6 0.20524667 0.09866418 22 (8,9] Male 1 16
#R> 13 -0.15501755 0.12045411 19 (8,9] Female 2 16
#R> 7 0.17958915 0.08401601 274 (9,9.97] Male 1 17
#R> 14 -0.25708101 0.09966941 232 (9,9.97] Female 2 17
#R> d1a2:
#R> by bySorted
#R> 1 [3.25,4] 11
#R> 2 (4,5] 12
#R> 3 (5,6] 13
#R> 4 (6,7] 14
#R> 5 (7,8] 15
#R> 6 (8,9] 16
#R> 7 (9,9.97] 17
# A
tym1b_gr_unemp_breaks_sex$data.a
#R> atet atet.sd count by over overold bySorted
#R> 1 0.13854523 0.17418488 11 [3.25,4] Male 1 11
#R> 8 0.06313763 0.16342893 8 [3.25,4] Female 2 11
#R> 2 0.04016158 0.14429305 16 (4,5] Male 1 12
#R> 9 0.36804241 0.11160670 26 (4,5] Female 2 12
#R> 3 0.06252843 0.17917111 96 (5,6] Male 1 13
#R> 10 0.31142244 0.13154404 102 (5,6] Female 2 13
#R> 4 0.09026293 0.12570475 128 (6,7] Male 1 14
#R> 11 0.27278924 0.14304280 186 (6,7] Female 2 14
#R> 5 0.12946909 0.09386141 283 (7,8] Male 1 15
#R> 12 -0.02607691 0.12604353 287 (7,8] Female 2 15
#R> 6 0.20524667 0.09866418 22 (8,9] Male 1 16
#R> 13 -0.15501755 0.12045411 19 (8,9] Female 2 16
#R> 7 0.17958915 0.08401601 274 (9,9.97] Male 1 17
#R> 14 -0.25708101 0.09966941 232 (9,9.97] Female 2 17
tym1b_gr_unemp_breaks_sex$plot.a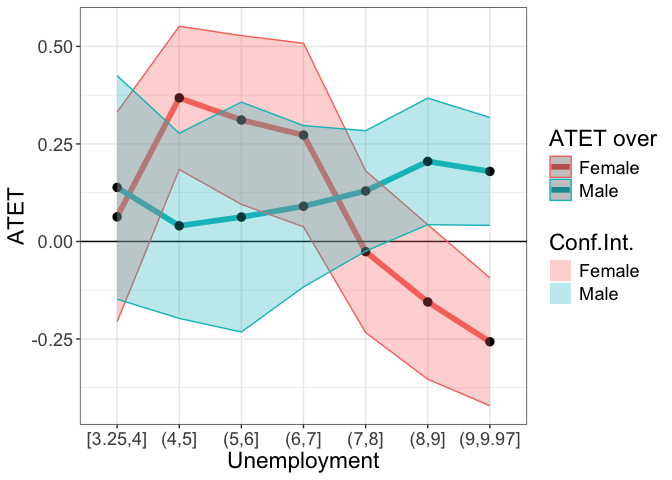
# B
tym1b_gr_unemp_breaks_sex$data.b
#R> atet atet.sd count by over overold bySorted
#R> 1 0.13854523 0.17418488 11 [3.25,4] Male 1 11
#R> 12 0.06313763 0.16342893 8 [3.25,4] Female 2 11
#R> 2 0.04016158 0.14429305 16 (4,5] Male 1 12
#R> 13 0.32885483 0.11108723 27 (4,5] Female 2 12
#R> 3 0.06164566 0.17819887 97 (5,6] Male 1 13
#R> 14 0.32860643 0.13221780 106 (5,6] Female 2 13
#R> 4 0.08969653 0.12484310 134 (6,7] Male 1 14
#R> 15 0.27417561 0.14359173 188 (6,7] Female 2 14
#R> 5 0.12961801 0.09338113 295 (7,8] Male 1 15
#R> 16 -0.02620078 0.12531064 307 (7,8] Female 2 15
#R> 6 0.14033220 0.09453717 164 (8,9] Male 1 16
#R> 17 -0.16251668 0.12633197 171 (8,9] Female 2 16
#R> 7 0.17531574 0.08320480 330 (9,10] Male 1 17
#R> 18 -0.26574815 0.09987550 286 (9,10] Female 2 17
#R> 8 0.19875742 0.13870169 56 (10,11] Male 1 18
#R> 19 -0.13154181 0.16909861 42 (10,11] Female 2 18
#R> 9 -0.03548073 0.34293848 192 (11,12] Male 1 19
#R> 20 -0.34540341 0.22072871 179 (11,12] Female 2 19
#R> 10 -0.00614826 0.38551391 129 (12,13] Male 1 20
#R> 21 -0.41261642 0.28848880 112 (12,13] Female 2 20
#R> 11 -0.05335951 0.37246881 16 (13,13.7] Male 1 21
#R> 22 -0.38001521 0.38901319 12 (13,13.7] Female 2 21
tym1b_gr_unemp_breaks_sex$plot.b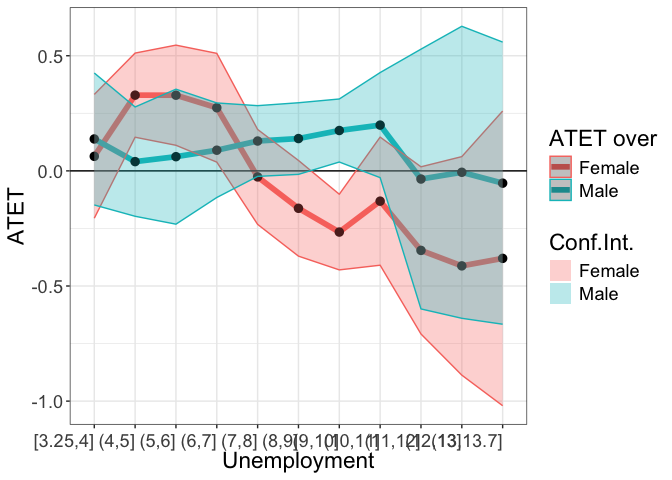
# ggsave(paste0("atet_ci_unemp_sex_breaks.pdf"), width = 15, height = 10, units = c("cm"))